The health index (HI) approach has been adopted widely as a tool to help asset managers prioritize their plans and actions. However, the conventional computation of HI, which is based on scoring and ranking, has several drawbacks. In this work, the fuzzy logic approach is used to build up an intelligent HI system to assess the condition of power transformers based on oil quality and DGA results.
The continuous demand to optimize the lifetime cost of transformers through informed decisions has led to adopting condition monitoring tools in addition to traditional offline testing methods. Many utilities have migrated from conventional time-based to condition-based maintenance. The outcome of the current diagnostic methods — online and offline — is large volumes of accumulated data. As a result, the use of quantitative indicators such as HI is gaining wide popularity, especially when it comes to prioritizing maintenance and replacement activities.
HI is an approach that combines all the information from a transformer to provide a single quantitative index that expresses overall condition based on measured data. The available data can be online, offline, operational, from condition monitoring systems, or from visual inspection, etc.
Several methods have been developed to convert existing diagnostic data into an HI. For instance, binary logistic regression is used in[1] for this purpose. The input data are classified into categories: healthy or unhealthy. Weights, assigned to each input, are calculated using the maximum likelihood criterion. Another approach is introduced in[2-5] to calculate the HI using the weighting average:
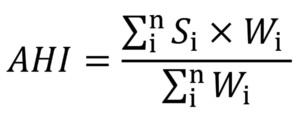
(1)
where:
n is the number of diagnostic tests
S is the score of each test measurement
W is the allocated weight given to each diagnostic test
In another work[6], the weighting sum is used instead to calculate the HI.
Despite the simplicity of weighting methods, determination of the weight factors for the diagnostic tests is based on the experience of experts, which differs from one person to another. In addition, setting a sharp threshold of diagnostic measurements for scoring is very difficult. In practice, scores can overlap. ISO/IEC Guide 98-3:2008 notes that an exact measurand does not exist due to the unavoidable imperfection involved in the measurement process.[7]
Moreover, experience shows that the traditional weighting average method may omit the influence of a bad diagnostic test result on overall health condition.
To address these challenges, artificial intelligence (AI) has been applied as an alternative approach to calculate HI. For example, the artificial neural network (ANN) in[8] and the adaptive neuro-fuzzy inference system (ANFIS) in[9] are used to evaluate the HI of transformers. However, their practical application in electric utilities is scarce due to the challenges associated with symbolic reasoning and preparing large amounts of hand-crafted, structured training data.
In this article, fuzzy logic is utilized to build up an intelligent model for evaluating the HI of power transformers. Contrary to ANN and ANFIS, fuzzy logic is based on a network of if-then rules that are constructed using the experience of experts. Fuzzy logic does not need to learn training data, and it has sophisticated capability to process the rules for all possible scenarios and form an accurate decision. Additionally, fuzzy logic does not apply sharp thresholds between the grades of the input data, since imprecision and fuzziness are the core of the fuzzy set theory.
USING OIL ANALYSIS TO ASSESS POWER TRANSFORMER CONDITION
Conventionally, the primary areas of concern for electric utilities are oil quality and DGA results. Because oil sampling is the most practical way to diagnose the condition of transformers while they are in service, the scope of this work is focused on oil quality and DGA results. However, the proposed fuzzy logic model can be similarly extended to include all the possible factors that impact transformer condition.
Disolved Gas Analysis
The analysis of dissolved gases in a transformer’s oil gives general information on the condition of the transformer and identifies unusual events such as incipient faults. Gases such as methane (CH4), ethane (C2H4), hydrogen (H2), ethylene (C2H6), acetylene (C2H2), carbon monoxide (CO), and carbon dioxide (CO2) are analysed to determine the types and severity of each fault.
Oil Quality
Oil quality tests focus on the condition of oil and paper insulation. Several parameters are usually monitored for oil, including break-down voltage (BDV), acidity, water content, interfacial tension (IFT), and furanic compounds such as 2-FAL.
FUZZY LOGIC APPROACH
Figure 1 shows the architecture of the fuzzy logic process, which consists of three stages.
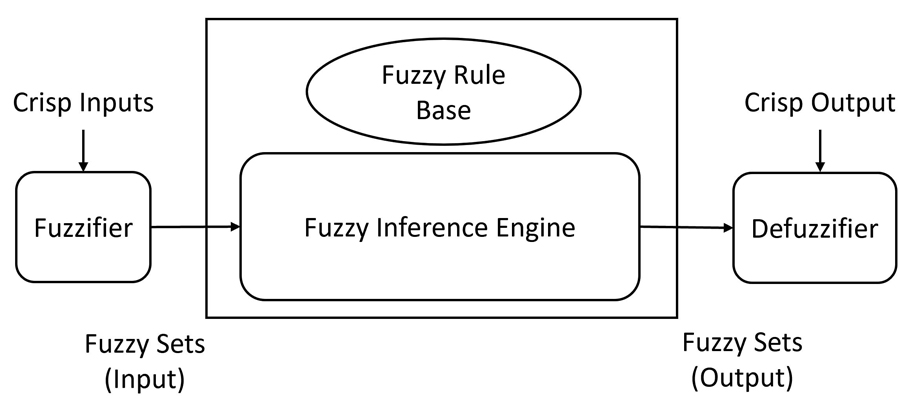
Figure 1: Block Diagram of the Fuzzy Logic Process
Fuzzification
The truth of any statement in fuzzy logic is just a matter of degree. This degree of truth is determined by generating membership functions (MF). MF is a curve or straight line that defines how a given input is mapped to a degree of membership between 0 and 1 of the fuzzy sets. It can be triangular, trapezoidal, sigmoidal, or Gaussian. The MF used in this work is trapezoidal, as shown in Figure 2, because of its simplicity. It is expressed as in (2):
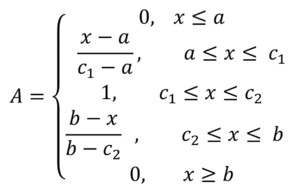
(2)
where:
x is the input parameter
If x lies between the centres of the trapezoidal c₁ and c₂, then the corresponding MF achieves the maximum degree of membership of 1. On the other hand, if the input is between a and c₁ or b and c₂, then the degree of membership is less than 1. This is the case when the measurand of a diagnostic test lies near the thresholds.
In this stage, the MFs convert the inputs from precise to fuzzy form between 0 and 1.
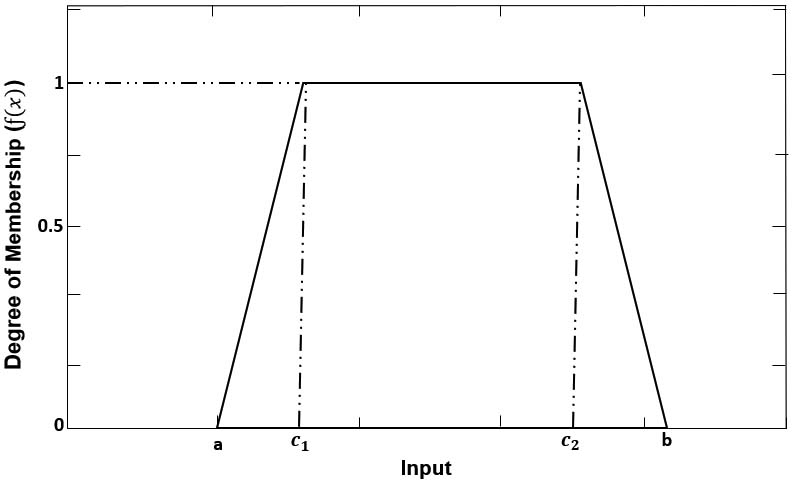
Figure 2: Trapezoidal Membership Function
Fuzzy Rules and Fuzzy Inference Engine
This work uses the Mamdani fuzzy inference system. It is described in the XY−plane as:
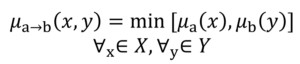
(3)
where:
μa(x) is the membership function of fuzzy set a defined in universe X
μb(y) is the membership function of fuzzy set b defined in universe Y
μa→b(x, y) is the fuzzy implication in XY-plane
The min (μa(x), μb(y)) takes the minimum of the two (or more) membership values when fuzzy rules are fired.
Meanwhile, fuzzy rules are a set of knowledge-based linguistic rules developed by the knowledge of test data interpretation and its impact on the condition of transformers. For instance, some of the implemented rules for arcing in the oil of transformers are:
- If (C2H2 is very high) and (H2 is very high), then (arcing is very high).
- If (C2H2 is very high) and (H2 is high), then (arcing is very high).
- If (C2H2 is medium) and (H2 is high), then (arcing is high).
- If (C2H2 is low) and (H2 is medium), then (arcing is medium).
In this stage, the results of the rules are combined to form the final value — a fuzzy value.
Defuzzification
In this work, defuzzification using the centroid method is performed. It determines the centre of gravity (Z0) of the area bound by the truncated output MFs, as in (4):
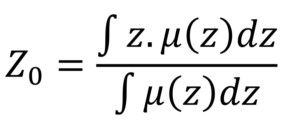
(4)
where:
z is the output variable
μ(z) is the degree of membership of the truncated output MF.
ADOPTING FUZZY LOGIC TO ASSESS TRANSFORMER CONDITION
The proposed HI modelling based on the oil results is shown in Figure 3. In the proposed architecture, the HI of the transformer is divided into three main failure profiles: prognostic index (PI), oil quality index (OQI), and dissolved gas analysis index (DGAI). The score of each failure profile is evaluated based on the scores of the associated failure modes.
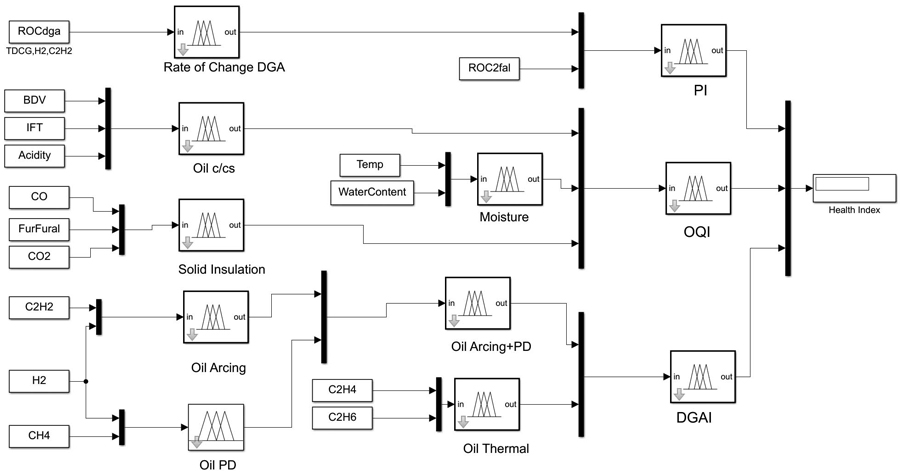
Figure 3: Fuzzy Logic Architecture of HI Evaluation
DGA Index (DGAI)
DGAI is based on the results of the levels of gases in the oil. The level of each gas is subsequently fuzzified into four fuzzy sets (MFs): low, medium, high, and very-high (VHigh), respectively. As an example, the MF of H2 is shown in Figure 4.
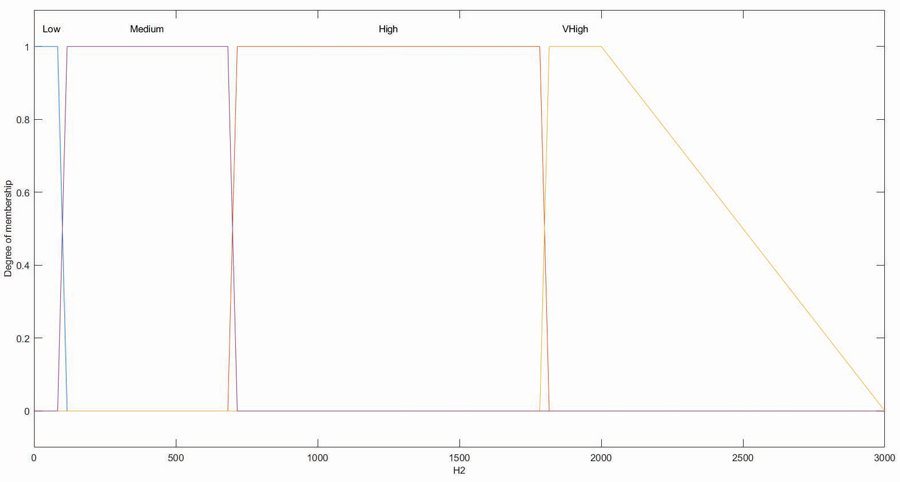
Figure 4: Membership Function of H2 Gas
The lower and upper limits and the two centres for each of the seven MFs for each input gas concentration are given in Table 1. The lower and upper limits were selected in accordance with IEEE Std C57.10–2008[10].
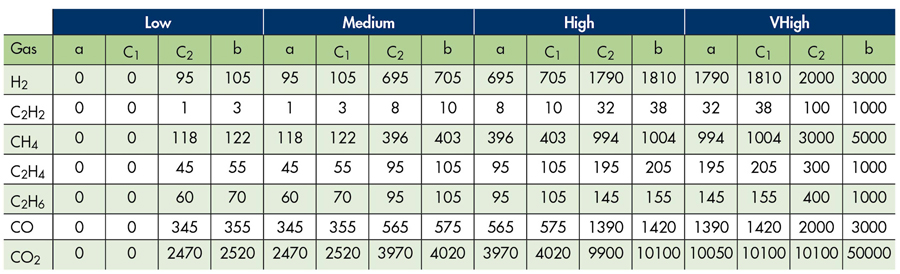
Table 1: Limit Values of Gas Concentration MFs
The DGAI index is composed of two main modules: oil arcing and PD, and oil thermal (Figure 5). Due to the thermal effect, the transformer’s oil decomposes and generates ethylene and ethane as principal gases. Therefore, one module was created for both ethylene and ethane to represent the oil thermal failure mode.
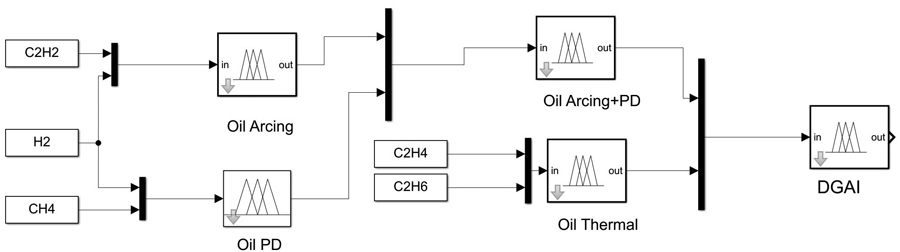
Figure 5: DGAI Module
On one hand, the presence of hydrogen and acetylene in the oil may indicate arcing. Based on transformer diagnostic and test data interpretation techniques, fuzzy rules are developed for the oil arcing sub-module (Figure 6).
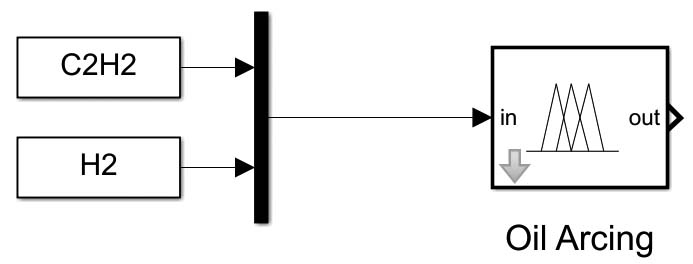
Figure 6: Oil Arcing Sub-Module
The three-dimensional curve plotted in Figure 7 shows the oil arcing output score (z-axis), which is based on the values of hydrogen, acetylene, their corresponding membership functions, and the predefined fuzzy rules of the oil arcing sub-module. The oil arcing output score is divided into four categories: very-high (yellow), high ( green), medium (light blue), and low (dark blue).
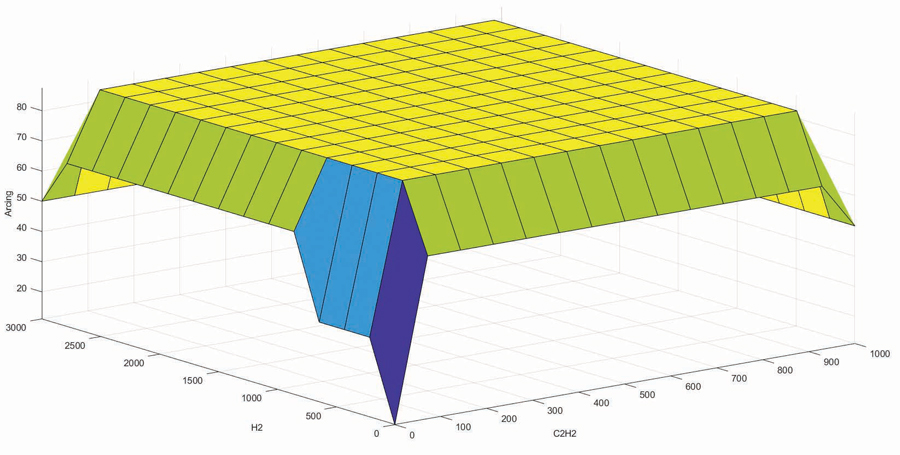
Figure 7: Scoring of Oil Arcing Sub-Mode Based on H2 and C2H2
On the other hand, partial discharge (PD) activity in a transformer produces a high level of hydrogen and a considerable level of methane gases. An individual sub-module for oil PD is designed and combined with the sub-module oil-arcing mode so the output score of both sub-modules reflects the oil-arcing and PD failure module.
Prognostic Index (PI)
The inputs to the PI module, shown in Figure 8, are data that change with respect to time. The monotony increase of the input values gives an indication of the deterioration of the transformer’s condition. MFs are developed for the daily generated ppm of TDCG, hydrogen, and acetylene.
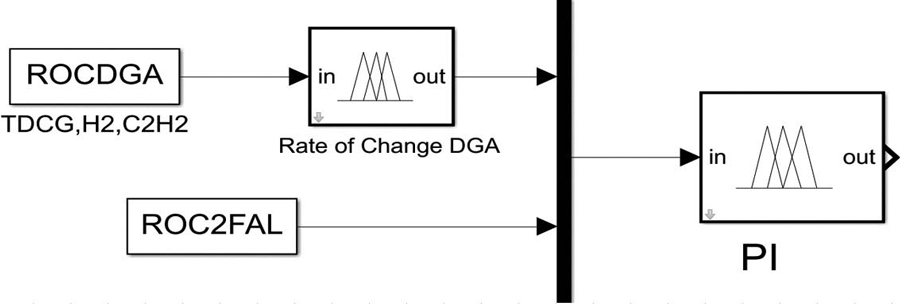
Figure 8: Prognostic Index Profile
The fuzzy inference system of the inputs is indicated in Figure 9, which shows 29 of the 64 implemented fuzzy rules. These rules cover all possible scenarios of the input data and the associated output score. For example, when the daily rate of change (ROC) of C2H2 = 2.3, H2 = 2.3, and TDCG = 9.79, Rule 25 is fired, and the output score of the ROC DGA module shown in Figure 8 is 87.5.
Figure 9: Fuzzy Inference Rules of ROC DGA Module
In addition, MFs are created to include the ROC of 2FAL for thermally upgraded paper, in ppm per year, such that the output score of the ROC of DGA sub-module and the ROC of furfural are inputs to the PI profile.
Oil Quality Index (OQI)
OQI is a combination of three modules for moisture, oil characteristics, and solid insulation, as shown in Figure 10. MFs are developed for the input data: break down voltage (BDV), acidity, interfacial tension (IFT), water content, oil temperature, CO, CO2, and the absolute value of 2FAL. Since the water content values (in ppm) are dependent on oil temperature, a separate module for moisture is used with its own implemented fuzzy rules, and the output of moisture module is the input to OQI.
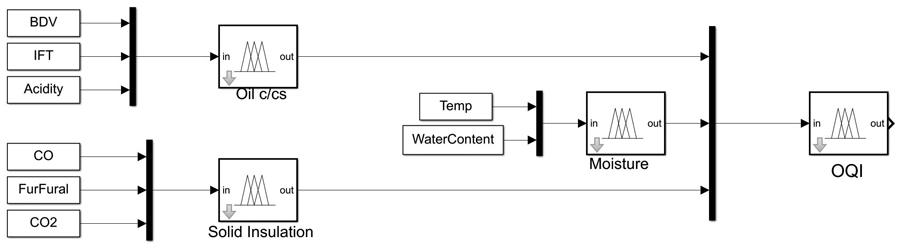
Figure 10: Fuzzy Logic — Oil Quality Index
The output score of the oil characteristics module is based on the three inputs of BDV, acidity, and IFT. The BDV test is one of the prominent diagnostic tests. This test gives an indication of contaminants, such as oil degradation products and water. Acidity in the oil deteriorates the dielectric properties of paper insulation and accelerates the oxidation process in the oil. Increased oil acidity in a transformer indicates the rate of degradation of the oil with sludge. The output of the oil characteristics module is an input of the OQI module.
Similarly, the solid insulation module output depends on CO and CO2 gas levels in addition to the absolute value of 2FAL in the oil.
CONCLUSION
The fuzzy logic method is utilized to build up an intelligent system to evaluate the condition of power transformers based on oil data. Hundreds of fuzzy rules have been developed in the proposed model to mimic the behavior of an oil transformer expert and generate a reliable health index. The proposed model can be a useful tool to make decisions and prioritize power transformer maintenance plans.
This article was first published in Transformers Magazine, Special Edition, Digitalization, November 2020, www.transformers-magazine.com.
REFERENCES
[1] W. Zuo, H. Yuan, Y. Shang, Y. Liu, T. Chen. “Calculation of a health index of oil-paper transformers insulation with binary logistic regression,” Mathematical Problems in Engineering, Vol. 2016, 2016.
[2] I. Hernanda, A. Mulyana, D. Asfani, I. Negara, D. Fahmi. “Application of health index method for transformer condition assessment,” Annual International TENCON Conference, Thailand, 2015.
[3] A. Naderian, S. Cress, R. Piercy, F. Wang, J. Service. “An Approach to determine the health index of power transformers,” Conference Record of the 2008 IEEE International Symposium on Electrical Insulation, pp. 192-196, 2008.
[4] F. Ortiz, I. Fernandez, A. Ortiz, C. J. Renedo, F. Delgado, C. Fernandez. “Health indexes for power transformers: A case study,” IEEE Electrical Insulation Magazine, Vol. 32, pp. 7-17, 2016.
[5] A. Jahromi, R. Piercy, S. Cress, J. Service, W. Fan. “An approach to power transformer asset management using health index,” IEEE Electrical Insulation Magazine, Vol. 25, no. 2, pp. 20-34, March-April 2009.
[6] R. J. Heywood, T. McGrail. “Clarifying the link between data, diagnosis and asset health indices,” IET Conference Publications, 2015.
[7] ISO/IEC Guide 98-3:2008, Uncertainty of measurement, Part 3: Guide to the expression of uncertainty in measurement, 2008.
[8] P. H. Mukti, F. A. Pamuji, B. S. Munir. “Implementation of artificial neural networks for determining power transfomer condition,” 5th International Symposium on Advanced Control of Industrial Processes (ADCONIP 2014), pp. 473-477, 28–30 May, 2014.
[9] H. Zeinoddini-Meymand, B. Vahidi. “Health index calculation for power transformers using technical and economical parameters,” IET Science, Measurement & Technology, Vol. 10, no. 7, pp. 823-830, 10 2016.
[10] IEEE Std C57.104-2008, IEEE Guide for the Interpretation of gases generated in oil-immersed transformers, 2008.
Mohamed Khalil is a Technical Application Engineer at Doble Engineering, focusing on Doble’s enterprise asset management solutions. His fields of interests are reliability evaluation of electrical systems, failure modes, and criticality analysis. He was appointed to the IEEE Instrumentation and Measurement Administrative Committee and was a guest editor of IEEE Instrumentation and Measurement Magazine. Mohamed is currently an invited technical reviewer in a number of IEEE conferences. He received his M.Sc. in electrical engineering and his PhD in reliability engineering from Politecnico di Milano, Italy.